Observation Selection Theory and Cosmological Fine-tuning

When our measurement instruments sample from only a subspace of the domain that we are seeking to understand, or when they sample with uneven sampling density from the target domain, the resulting data will be affected by a selection effect. If we ignore such selection effects, our conclusions may suffer from selection biases.

A classic example of selection bias is the election poll taken by the Literary Digest in 1936. On the basis of a large survey, the Digest predicted that Alf Langdon, the Republican presidential candidate, would win by a large margin. But the actual election resulted in a landslide for the incumbent, Franklin D. Roosevelt. How could such a large sample yield such a wayward prediction? The Digest, it turned out, had harvested the addresses for its survey mainly from telephone books and motor vehicle registries. This introduced a strong selection effect. The poor of the depression era, a group that disproportionally supported Roosevelt, often did not have phones or cars.

The Literary Digest suffered a major reputation loss and soon went out of business. It was superseded by a new generation of pollsters, including George Gallup, who not only got the 1936 election right but also managed to predict what the Digest’s prediction would be to within 1%, using a sample that was only one thousandth as large. The key to Gallup’s success lay in his accounting for known selection effects. Statistical techniques are now routinely used to correct for many kinds of selection bias.

Observation selection effects are an especially subtle kind of selection effect that is introduced not by limitations in our measurement apparatuses but by the fact that all evidence is preconditioned on the existence of an observer to “have” the evidence and to build the instruments in the first place. Only quite recently have observation selection effects become the subject of systematic study. Observation selection effects are important in many scientific areas, including cosmology and parts of evolution theory, thermodynamics, the foundations of quantum theory, and traffic analysis. There are also interesting applications to the search for extraterrestrial life and questions such as whether we might be living in a computer simulation created by an advanced civilization [1].

Observation selection theory owes a large debt to Brandon Carter, a theoretical physicist who wrote several seminal papers on the subject, the first one published in 1974 [2-5]. Although there were many precursors, one could fairly characterize Carter as the father of observation selection theory – or “anthropic reasoning” as the field is also known. Carter coined the “weak” and the “strong anthropic principle”, intending them to express injunctions to take observation selection effects into account. But while Carter knew how to apply his principles to good effect, his explanation of the methodology they were meant to embody was less than perfectly clear. The meaning of the anthropic principles was further obscured by some later interpreters, who endowed them with additional content quite unrelated to observation selection effects. This contraband content, which was often of a speculative, metaphysical, or teleological nature, caused “anthropic” reasoning to fall into disrepute.[1] The confusion about what anthropic reasoning is about continues to the present day, although there seems to be a growing recognition in the last few years that it is on to something interesting and legitimate.

Since Carter’s pioneering explorations, considerable effort has been devoted to working out the applications of anthropic principles, especially as they pertain to cosmological fine-tuning. There have also been many philosophical investigations into the foundations of anthropic reasoning. These investigations have revealed several serious paradoxes, such as the Doomsday argument [9], the Sleeping Beauty problem [10] [11], and the Adam and Eve and the UN⁺⁺ thought experiments [12]. It is still controversial what conclusions we should draw from the apparent fine-tuning of our universe, as well as whether and to what extent our universe really is fine-tuned, and even what it means to say that it is fine-tuned.

Developing a theory of observation selection effects that caters to legitimate scientific needs while sidestepping the paradoxes is a non-trivial challenge. In my recent book Anthropic Bias: Observation Selection Effects in Science and Philosophy, I presented the first mathematically explicit general observation selection theory and examined some of its implications.

Before sketching some of the basic elements of this theory and illustrating how it applies to the multiverse hypothesis, let us briefly consider some of the difficulties that such a theory must overcome.

2. The need for a probabilistic anthropic principle

The anthropic principles proposed by Carter, even setting aside the inadequacies of his formulations, were insufficiently strong for many scientific applications. A key shortcoming is that they were not probabilistic.

Carter’s principles enable us to handle some straightforward cases. Consider a simple theory that says that there are 100 universes, and that 90 of these are lifeless and 10 contain observers. What does such a theory predict that we should observe? Clearly not a lifeless universe. Since lifeless universes contain no observers, an observation selection effect, as enunciated by the strong anthropic principle, precludes them from being observed. Although the theory claims that the majority of universes are lifeless, it nevertheless predicts that we should observe one of the atypical universes that contain observers.

Let’s take a slightly more complicated case. Suppose a theory says that there are 100 universes of the following description:

What does this theory predict that we should observe? (We need to know the answer to this question in order to determine whether it is confirmed or disconfirmed by our observations.) As before, an obvious observation selection effect precludes type-A universes from being observed, so the theory does not predict that we should observe one of those. But what about type-B and type-C universes? It is logically compatible with the theory that we should be observing a universe of either of these kinds. However, probabilistically it is more likely, conditional on the theory, that we should observe the type-C universe, because that is what the theory says that over 99% of all observers observe. Finding yourself in a type-C universe would, ceteris paribus, tend to confirm such a theory, to at least some degree, compared to other theories that imply that most observers live in type-A or type-B universes.

To get this result, we must introduce a probabilistic strengthening of the anthropic principle along the lines of what I have called the Self-Sampling Assumption [11, 13, 14]:

With the help of SSA, we can calculate the conditional probabilities of us making a particular observation given one theory or another, by comparing what fraction of the observers in our reference class would be making such observations according to the competing theories.

What SSA does is enable us to take indexical information into account. Consider the following two evidence statements concerning the current temperature of the cosmic microwave background radiation (CMB)[3]:

Note that E* implies E, but not vice versa. E*, which includes a piece of indexical information, is logically stronger than E. It is consequently E* that dictates what we should believe in case these different evidence statements lead to different conclusions. This is a corollary of the principle that all relevant information should be taken into account.

Let us examine a case where it is necessary to use E* rather than E [21]. Consider two rival theories about the local temperature of CMB. Let T₁ be the theory we actually hold, claiming that CMB = 2.7K. Let T₂ say that CMB = 3.1K. Now, suppose that the universe is infinitely large and contains an infinite number of stochastic processes of suitable kinds, such as radiating black holes. If for each such random process there is a finite, non-zero probability that it will produce an observer in any particular brain state (subjectively making an observation e), then, because there are infinitely many independent “trials”, the probability, for any given observation e, that e will be made by some observer somewhere in the universe is equal to 1. Let B be the proposition that this is the case. We might wonder how we could possibly test a conjunction like T₁&B, or T₂&B. For whatever observation e we make, both these conjunctions predict equally well (with probability 1) that e should be made. According to Bayes’s theorem, this entails that conditionalizing on e being made will not affect the posterior probability of T₁&B, or of T₂&B. And yet it is obvious that the observations we have actually made support T₁&B over T₂&B, for, needless to say, it is because of our observations that we believe that CMB = 2.7K and not 3.1K.

The problem is solved by using the stronger evidence statement E* and applying SSA. For any reasonable choice of reference class, T₁&B implies that a much larger fraction of all observers in that class should observe CMB = 2.7K than CMB = 3.1K, than does T₂&B. (According to T₁&B, all normal observers observe CMB = 2.7K, while on T₂&B only some exceptional black-hole-emitted observers, or those who suffer from rare illusions, or those who are witnessing a local thermal fluctuation, observe CMB = 3.1K.) Given these facts, SSA implies:

From (1) it is then easy to show that our actual evidence E* does indeed give us reason to believe T₁&B rather than T₂&B. In other words, SSA makes it possible for us to know learn that CMB = 2.7K.

In the foregoing reasoning, we have set aside the problem of exactly how the reference class is to be defined. In the above example, any reference class definition satisfying some very weak constraints would do the trick. To keep things simple, we have also ignored the problem of how to generalize SSA to deal with infinite domains. Strictly speaking, such an extension, which might involve focusing on densities rather than sets of observers, would be necessary to handle the present example.[4]

Since 90% of all observers are in blue cells, and you don’t have any other relevant information, it seems that you should set your credence (your subjective probability) of being in a blue cell to 90%. Most people seem to agree that this is the correct answer. Since the example does not depend on the exact numbers involved, we have the more general principle that in cases like this, your credence of having property P should be equal to the fraction of observers who have P. You reason as if you were a randomly selected observer, in accordance with SSA.

While many accept without further argument that SSA is applicable to Dungeon, it may be useful briefly to consider how this view could be defended if challenged. One argument one can adduce is the following. Suppose that everyone accepts SSA and everyone has to bet on whether they are in a blue or a red cell. Then 90% of the prisoners will win their bets; only 10% will lose. If, on the other hand, SSA is rejected and the prisoners think that one is no more likely to be in a blue cell than in a red cell, and they bet, for example, by flipping a coin, then on average merely 50% of them will win and 50% will lose. It seems better that SSA be accepted.

What allows the people in Dungeon to do better than chance is that they have a relevant piece of empirical information regarding the distribution of observers over the two types of cells; they have been informed that 90% are in blue cells. It would be irrational not to take this information into account. We can imagine a series of thought experiments where an increasingly large fraction of observers are in blue cells – 91%, 92%, …, 99%. As the situation gradually degenerates into the limiting 100%-case where they are simply told, “You are all in blue cells,” from which each prisoner can deductively infer that he is in a blue cell, it is plausible to require that the strength of prisoners’ beliefs about being in a blue cell should gradually approach probability one. SSA has this property.

It is worth pointing out that we did not specify how the prisoners arrived in their cells. The prisoners’ history is irrelevant so long as they do not know anything about it that gives them clues about the color of their cells. For example, they may have been allocated to their respective cells by some objectively random process such as by drawing balls from an urn (while blindfolded so they could not see where they ended up). But the thought experiment does not depend on there being a well-defined randomization mechanism. One may just as well imagine that prisoners have been in their cells since the time of their birth, or indeed since the beginning of the universe. If there is a possible world in which the laws of nature determine, without any appeal to initial conditions, which individuals are to appear in which cells and how each cell is painted, then the inmates would still be rational to follow SSA, provided only that they did not have knowledge of the laws or were incapable of deducing what the laws implied about their own situation. Objective chance, therefore, is not an essential ingredient of the thought experiment. It runs on low-octane subjective uncertainty.

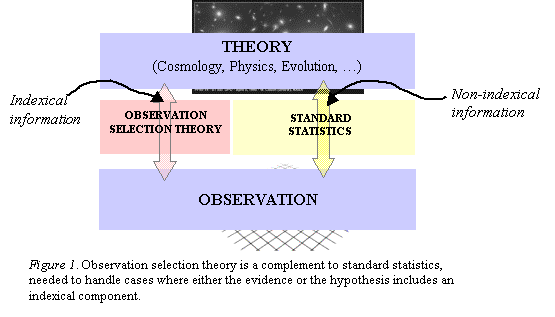
We see that there are contexts in which we need to take indexical information into account in order to connect theory with observation. We need a theory of how to do so. This is represented by the box complementing “standard statistics” in figure 1.

3. Challenges for observation selection theory

The reasoning embodied in SSA receives support from thought experiments and from its utility in helping to make sense of apparently legitimate scientific inferences. However, if we use SSA with what may seem like the most natural choice of reference class, the universal reference class consisting of all intelligent observers, we encounter paradoxes. One of these is the Doomsday argument, which purports to show that we have systematically underestimated the probability of impending extinction for our species.

Suppose that a large urn filled with consecutively numbered balls is placed in front of you. The urn might contain either ten balls or a million balls. If you randomly select a ball from the urn, and you find that it is ball number 7, that gives you strong evidence for the hypothesis that the urn contains only ten balls. Analogously, if you use the SSA with the universal reference class, thus reasoning as if you were a random sample from the class of all observers that will ever have lived, you can calculate the conditional probabilities, given various hypothesis about the total size of the human species, of this random sample having the particular “birth rank” that you have (i.e. your position in the sequence of all humans that will ever have lived).[5] For example, if you consider two hypotheses about how many humans there will have been (200 billion, or 200 trillion), and your birth rank is number 60 billion, then the SSA with the universal reference class implies that the conditional probability of you having rank 60 billion is a thousand times greater on hypothesis “total = 200 billion” than on the hypothesis “total = 200 trillion”. After Bayesian conditionalization on this piece of information about your birth rank, you find that “total = 200 billion” has gained dramatically in probability relative to its more optimistic alternative.[6]

The Doomsday argument does not imply any particular probability of impending extinction because the posterior probability of “doom soon” depends also on the empirical prior that we start out with. This prior should take into account factors such as our best guesses about the risks of germ warfare, nuclear war, meteor strikes, destructive nanotechnology, etc. Nevertheless, independently of the particular prior used, the posterior will be systematically skewed in favor of more pessimistic hypotheses. The posterior probability of our descendants ever colonizing the galaxy would be truly dismal for any plausible prior, as this would make our own place in human history highly atypical.

The most common initial reaction to the Doomsday argument is that it must be wrong. Moreover, it is typically asserted that it is wrong for some obvious reason. However, when it comes to explaining why it is wrong, it turns out that there are almost as many explanations as there are disbelievers, and the explanations tend to be mutually inconsistent. On closer inspection, all these objections, which allege some trivial fallacy, appear to be mistaken [9, 11, 22].

The Doomsday argument has its backers as well as detractors, and while the manner in which it purports to derive its conclusion is counterintuitive, it may not quite qualify as a paradox. It is therefore useful to consider the following thought experiment [12]. It has the same structure as the Doomsday argument but yields a conclusion that is even harder to accept.

It is easy to verify that, if we apply SSA to the universal reference class, the serpent’s mathematics is watertight. Yet surely it would be irrational for the couple to conclude that the risk of Eve becoming pregnant is negligible. Note that the inference would hold even if the couple, based on a detailed understanding of the biology of human reproduction, assigned a substantial prior probability of pregnancy (e.g. p > 1%).

One could try to revise SSA in various ways or impose stringent conditions on its applicability. It is difficult, however, to formulate a principle that satisfies all constraints that an observation selection theory ought to respect – a principle that serves legitimate scientific needs and at the same time is probabilistically coherent and paradox-free.[7]

Perhaps the most elegant maneuver to get rid of the Doomsday argument and the counterintuitive implication in the Serpent’s Advice thought experiment is to adopt what I have called the Self-Indication Assumption.

The beauty of SIA is that if we adopt it, we can keep using an unrestricted SSA with the universal reference class and still completely avoid the doomsday-like implications that follow from using SSA on its own without SIA. The idea is simple. First, you take into account the fact that you exist, which according to SIA gives you evidence in favor of many observers existing. Second you take into account your birth rank, which according to SSA gives you evidence in favor of few observers existing. It can be shown that these two probability shifts cancel out exactly, restoring the empirical prior probability of “doom soon”. This cancellation will result if we interpret SIA as asserting that the conditional probability of you finding yourself alive, given some hypothesis h, is proportional to the expected number of people that will have existed according to h.

In this thought experiment, there is no counterbalancing doomsday-like probability shift to cancel out the effect of SIA. This is because in Presumptuous Philosopher, the relevant “birth rank” is not know, i.e. our position in the sequence of all observers that will ever have existed throughout the universe. Without a low birth rank to conditionalize on, we are stuck with a seeming bias for thinking that the universe contains huge numbers of observers. If the prior empirical probability of the universe containing infinitely many observers were greater than zero, then after taking SIA into account it would climb to 100%, which is surely overconfidence. What is counterintuitive about SIA is not that we would have to accept that the universe is infinite – we might have independent reasons for that – but the grounds on which we should allegedly accept this, and the unreasonable level confidence that we would have in the conjecture.

4. Sketch of a solution

Perhaps the problem with SSA is not that it is too strong but that, in a way, it is not strong enough. SSA instructs you to take into account one kind of indexical information: information about which observer you are, but you have more indexical information than that. You also know which temporal segment of that observer – which “observer-moment” – you currently are. We can formulate a Strong Self-Sampling Assumption that integrates such temporal indexical information [11].

Arguments can be given that SSSA embodies a correct way of reasoning about a number of cases. For example, one can consider cases analogous to Dungeon but where the subject is ignorant about what time it is rather than about which room she is in.

The added analytical resolution provided by SSSA enables us to make a second move: relativizing the reference class. Rather than placing all observer-moments in the same reference class, we can use different reference classes for different observer-moments, to reflect the different information that may be available to observers at different times. For example, the early observer-moments of Adam and Eve might be placed in a different reference class from the observer-moments of other observers (or of themselves at later times). These later observer-moments would know whether Eve got pregnant or not, whereas the early observer-moments lack that knowledge. With such a relativized reference class, we would block the inference that Adam and Eve should assign a negligible probability to Eve getting pregnant, for whether she did or not, her early observer-moments would still be typical of their reference class, which now consists exclusively of such early observer-moments.[8]

It is tempting to surmise that the correct reference class to use for an observer-moment a is one that contains all and only those observer-movements that have exactly the same information as a. This minimal reference class would succeed in blocking the Serpent’s inference. However, such a reference class definition is too narrow to be correct in general. It would fail, for example, in the case of the two theories about the temperature of the cosmic background radiation. We observe CMB = 2.7K. On both T₁ and T₂, there would be some observers making that observation. If we restricted our reference class to those observers (or observer-moments) that have exactly the same information that we have, then – trivially – it would be the case that according to both T₁ and T₂, all observers in our reference class would observe CMB = 2.7K. The SSA would then specify the same conditional probability (unity) to our observation for both these theories. Hence our observation of CMB = 2.7K would fail to discriminate between the two theories, which is clearly not the case – we know that our observing CMB = 2.7K gives us evidence in favor of T₁. This shows that the minimal reference class definition is too narrow. A wider reference class must be used to make sense of scientific practice.

One is led to wonder whether there is a general rule for selecting a suitable reference class. While this is to some extent still an open question, my suspicion is that there might be not such rule. We can establish constraints on permissible choices of reference class. We have already seen two examples of such constraints: the correct reference class definition is narrower than the universal reference class and wider than the minimal reference class described above. Perhaps additional constraints could be discovered. But we might find that the full set of binding constraints will still underdetermine the choice of reference class.

The reference class in effect determines a prior over indexical belief. It is quite widely accepted that the traditional constraints of rationality fail to determine a uniquely correct prior over non-indexical belief – there seems to be an unavoidable element of subjectivity in the choice of prior over non-indexical belief. If in some cases there are more than one rationally defensible choice of reference class, this would merely show that the situation with regard to indexical belief is similar to what we already have accepted is the case with regard to non-indexical belief.

Different applications of “anthropic reasoning” makes different assumptions about the reference class. Some applications require only very weak assumptions: they would work given practically any (non-gerrymandered) choice of reference class. Other applications rely on much stronger assumptions about the reference class. For example, in the case of the temperature of the cosmic background radiation, we can use almost any reference class that is at least slightly more inclusive than the minimal reference class. The result we get does not depend on which of the many possible reference classes we choose. By contrast, the Serpent’s reasoning requires a rather particular kind of reference class – one that is inclusive enough to contain the observer-moments of the people who would be born centuries later and who would be in very different epistemic situations from the pre-sin Adam and Eve. This difference in how strong assumptions an application makes on the reference class seems to be related to how intuitively compelling or rigorous the application is. The Serpent’s reasoning is highly non-compelling whereas the cosmologist’s inference from our observations about the cosmic background may well be rationally obligatory. (Other applications fall somewhere in between.) We might thus be able to account for our intuitions about the degree of rigorousness of different applications of anthropic reasoning partly on the basis of how robust they are under varying choices of reference class.[9] This finding again mirrors the situation with regard to non-indexical belief. A scientific argument that is such that a wide range of priors (ideally, all rationally defensible priors) would converge on assigning a hypothesis a high probability after taking the argument into account is a more rigorous scientific argument for that hypothesis than is an argument that is merely suggestive to some people who happen to hold a particular kind of prior. Robustness under a large class of priors, indexical or non-indexical, can be viewed as a hallmark of scientific objectivity.

The idea that is expressed vaguely in SSSA can be formalized into a precise principle that specifies the evidential bearing of a body of evidence e on a hypothesis h. I have dubbed this the Observation Equation [11]:

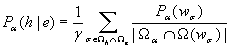
Here, is the observer-moment whose subjective probability function is . is the class of all possible observer-moments about whom h is true; is the class of all possible observer-moments about whom e is true; is the class of all observer-moments that places in the same reference class as herself; is the possible world in which is located; and is a normalization constant. The quantity in the denominator is the cardinality of the intersection of two classes, and , the latter being the class of all observer-moments that exist in the possible world .

The Observation Equation can be generalized to allow for different observer-moments within the reference class having different weights . This option is of particular relevance in the context of the many-worlds version of quantum mechanics, where the weight of an observer-moment would be proportional to the amplitude squared of the branch of the universal wavefunction where that observer-moment lives.

The Observation Equation expresses the core of a quite general methodological principle. Here we will just highlight two of its features by way of explication. The first is that by dividing the terms of the sum by the denominator, we are factoring out the fact that some possible worlds contain more observer-moments than do others. If one omitted this operation, one would in effect be assigning a higher prior probability to possible worlds that contain a greater number of observers (or more long-lived observers). This would be equivalent to accepting the Self-Indication Assumption, which prescribes an a priori bias towards worlds that have a greater population. As we have seen, arguments such as Presumptuous Philosopher suggest that SIA should be rejected.

A second feature is that the only observer-moments that are taken into account by an agent are those that the agent places in the same reference class as herself (at the time of the reasoning). For the purposes of taking into account indexical information, observer-moments outside of the reference class have the same status as rocks and other lifeless objects: epistemically, they are not relevant alternative indexical possibilities for the agent at the time.

5. Applications

Observation selection theory has applications outside philosophy. For example, when we ask about what our evidence tells us about how likely it was for intelligent life to evolve on Earth, or how many “critical steps” took place in the evolutionary process, or what the chances are that we will ever encounter extraterrestrial intelligence, we encounter observation selection effects that need to be taken into account. This also happens when we critically assess Boltzmann’s attempt to explain time’s arrow by postulating that we live in a vast local thermal fluctuation in a universe that as a whole is in thermal equilibrium. Observation selection effects also crop up in regard to certain questions in the foundations of quantum physics. Yet it is in cosmology that we find the best-known applications of anthropic reasoning.

As we saw earlier, observation selection theory is needed to derive any observational predictions whatever from “big world” cosmologies that imply the world is large enough and random enough that all possible human observations are, with probability one, in fact made.

A more specific application in cosmology pertains to the apparent fine-tuning of various physical constants and parameters. “Fine-turning” refers to the apparent fact that, for a number of physical parameters, had they had a value only very, very, slightly different from their actual value (on any intuitively plausible measure of “slightly”) then life could not have existed. It seems as though the world is balancing on a knife’s edge. This is puzzling: why should the world be like that?[10] The growing popularity of multiverse theories, according to which our universe is but one in a large ensemble of universes, is attributable in large measure to the hope that such theories can offer an “anthropic explanation” of the apparent fine-tuning. By allaying worries that anthropic reasoning is inherently flawed or paradox-ridden, observation selection theory puts these explanations on a firmer methodological footing.

Let us consider some more specific lessons. A multiverse theory can potentially explain cosmological fine-tuning, but only if several conditions are met. To begin with, the theory must assert the actual existence of an ensemble of physically real universes. (An ensemble of merely “possible universes” would not do.) The universes in this ensemble would have to differ from one another with respect to the values of the fine-tuned parameters, according to a suitably broad distribution. If observers can exist only in those universes in which the relevant parameters take on the observed fine-tuned values (or if the theory at least implies that a large portion of all observers are likely to live in such universes), then an observation selection effect can be invoked to explain why we observe a fine-tuned universe. Further, in order for the explanation to be completely satisfactory, the postulated multiverse should not itself be significantly fine-tuned, for otherwise the explanatory problem would merely have been postponed.

A multiverse theory meeting these requirements could give a relatively high conditional probability to our observing a fine-tuned universe. It would thereby gain a degree of evidential support from the finding that our universe is fine-tuned. Such a theory could also help explain why we find ourselves in a fine-tuned universe, but to do in this, the theory would also have to meet the ordinary set of methodological desiderata – it would have to be physically plausible, fit the evidence, be relatively simple and non-gerrymandered, and so forth. Determining whether this potential anthropic explanation of fine-tuning actually succeeds requires a lot of detailed work in empirical cosmology.

One may wonder whether these conclusions depend on fine-tuning per se or whether they follow directly from the generic methodological injunction that we should, other things being equal, prefer simpler theories with fewer free variables to more complex theories that require a larger number of independent stipulations to fix their parameters (Occam’s razor). In other words, how does the fact that life would not have existed if the constants of our universe had been slightly different play a role in making fine-tuning cry out for an explanation and in suggesting a multiverse theory as a possible answer?

Observation selection theory helps us answer these questions. It is not just that all single-universe theories currently in the offing would seem to require delicate handpicking of lots of independent parameter-values that would make such theories unsatisfactory: the fact that life would not otherwise have existed adds to the support for a multiverse theory. How does that fact do this? By making the anthropic multiverse explanation possible. A simple multiverse theory could potentially give a high conditional probability to us observing the kind of universe we do because it says that only that kind of universe, among all the universes in a multiverse, would be observed (or at least, that it would be observed by a disproportionately large fraction of the observers). The observation selection effect operating on the fact of fine-tuning concentrates the conditional probability on us observing a universe like the one we see.

Moreover, observation selection theory enables us to answer the question of how big a multiverse has to be in order to explain our evidence. The upshot is that bigger is not always better [11]. The postulated multiverse would have to be large and varied enough to make it probable that some universe like ours should exist. Once this size is reached, there is no additional anthropic ground for thinking that a theory that postulates an even bigger ensemble of universes is therefore, other things equal, more probable. The choice between two multiverse theories that both give a high probability to a fine-tuned universe like ours existing must be made on other grounds, such as simplicity or how well they fit with the rest of physics.

A multiverse would not have to be large enough to make it probable that a universe exactly like ours should exist. A multiverse theory that entails such a huge cosmos that one would expect a universe exactly like ours to be included in it does not have an automatic advantage over a more frugal competitor. Such an advantage would have to be earned, for instance by enabling greater simplicity. There is no general reason for assigning a higher probability to theories that entail that there is a greater number of observers in our reference class. Increasing the membership in our reference class might make it more likely that the reference class should contain some observer who is making exactly the observations that we are making, but it would also make it more surprising that we should happen to be that particular observer rather than one of the others in the reference class. The net effect of these two considerations is to cancel each other out. All the observation selection effect does is concentrate conditional probability on the observations represented by the observer-moments in our reference class so that, metaphorically speaking, we can postulate stuff outside the reference class “for free”. Postulating additional stuff within the reference class is not gratis in the same way but would have to be justified on independent grounds.

It is, consequently, in major part an empirical question whether a multiverse theory is more likely than a single-universe theory, and whether a larger multiverse is more plausible than a smaller one. Anthropic considerations are an essential part of the methodology for addressing these questions, but the answers will depend on the data.

References

1. Bostrom, N., "Are You Living in a Computer Simulation?," Philosophical Quarterly 53(211) (2003): pp. 243-55.

2. Carter, B., Large Number Coincidences and the Anthropic Principle in Cosmology, in Confrontation of Cosmological Theories with Data, M.S. Longair, Editor. 1974, Reidel: Dordrecht. pp. 291-298.

3. Carter, B., "The Anthropic Principle and its Implications for Biological Evolution," Philosophical Transactions of the Royal Society A 310 (1983): pp. 347-363.

4. Carter, B., The Anthropic Selection Principle and the Ultra-Darwinian Synthesis, in The Anthropic Principle, F. Bertola and U. Curi, Editors. 1989, Cambridge University Press: Cambridge. pp. 33-63.

5. Carter, B., Large Number Coincidences and the Anthropic Principle in Cosmology, in Physical Cosmology and Philosophy, J. Leslie, Editor. 1990, Macmillan Publishing Company.

6. Earman, J., "The SAP also rises: a critical examination of the anthropic principle," Philosophical Quarterly 24(4) (1987): pp. 307-317.

7. Gardner, M., "WAP, SAP, FAP & PAP," New York Review of Books 33(May 8) (1986): pp. 22-25.

8. Barrow, J.D. and F.J. Tipler, The Anthropic Cosmological Principle (Oxford: Oxford University Press, 1986).

9. Bostrom, N., "The Doomsday Argument is Alive and Kicking," Mind 108(431) (1999): pp. 539-550.

10. Bostrom, N., "Sleeping Beauty: A Synthesis of Views," working paper (2004): pp.

11. Bostrom, N., Anthropic Bias: Observation Selection Effects in Science and Philosophy (New York: Routledge, 2002).

12. Bostrom, N., "The Doomsday argument, Adam & Eve, UN++, and Quantum Joe," Synthese 127(3) (2001): pp. 359-387.

14. Bostrom, N., "Observer-relative chances in anthropic reasoning?," Erkenntnis 52 (2000): pp. 93-108.

15. Gott, R.J., "Implications of the Copernican principle for our future prospects," Nature 363(27 May) (1993): pp. 315-319.

16. Vilenkin, A., "Predictions From Quantum Cosmology," Physical Review Letters 74(6) (1995): pp. 846-849.

17. Page, D.N., "Sensible Quantum Mechanics: Are Probabilities Only in the Mind?," International Journal of Modern Physics D 5(6) (1996): pp. 583-596.

18. Page, D.N., Can Quantum Cosmology Give Observational Consequences of Many-Worlds Quantum Theory, in General Relativity and Relativistic Astrophysics, Eighth Canadian Conference, Montreal, Quebec, C.P. Burgess and R.C. Myers, Editors. 1999, American Institute of Physics: Melville, New York. pp. 225-232.

19. Tegmark, M., "Is 'the theory of everything' merely the ultimate ensemble theory?," Annals of Physics 270(3 Apr) (1998): pp. 1-51.

20. Linde, A. and A. Mezhlumian, "On Regularization Scheme Dependence of Predictions in Inflationary Cosmology," Phys.Rev. D 53 (1996): pp. 4267-4274.

21. Bostrom, N., "Self-Locating Belief in Big Worlds: Cosmology's Missing Link to Observation," Journal of Philosophy 99(12) (2002): pp. 607–623.

22. Leslie, J., The End of the World: The Science and Ethics of Human Extinction (London: Routledge, 1996).

24. White, R., "Fine-Tuning and Multiple Universes," Noûs 34:2 (2000): pp. 260-276.

25. Hacking, I., "The inverse gambler's fallacy: the argument from design. The anthropic principle applied to wheeler universes," Mind 76 (1987): pp. 331-340.

26. Swinburne, R., Argument from the fine-tuning of the universe, in Physical cosmology and philosophy, J. Leslie, Editor. 1990, Collier Macmillan: New York. pp. 154-73.

27. Whitaker, M.A.B., "On Hacking's criticism of the Wheeler anthropic principle," Mind 97(386) (1988): pp. 259-264.

28. McGrath, P.J., "The inverse gambler's fallacy," Mind 97(386) (1988): pp. 265-268.

29. Carlson, E. and E.J. Olsson, "Is our existence in need of further explanation?," Inquiry 41 (1998): pp. 255-75.

30. Manson, N.A., "There Is No Adequate Definition of 'Fine-tuned for Life'," Inquiry 43 (2000): pp. 341-52.

[1] See e.g. [6, 7]. Anthropic reasoning was first brought to the attention of a wider audience in [8].

[2] Related principles have also been explored in e.g. [15-18]; see also [19, 20].

[3] In this toy example, we assume that the “current time” is defined with reference to some other parameter of cosmological evolution than the temperature of the background radiation itself. To avoid this inelegancy, we could change the example and pick some stochastic constant, such as the half-life of some particle, and let T₁ and T₂ be two theories that make different assertions about the value of this constant.

[4] We could still make the present point by considering another example in which the universe is assumed to be finite but so big that both theories predict that observations of both temperatures will be made by some observers.

[5] Let us assume the simplest case here, that humanity is the only intelligent species in the world.

[6] Note that the argument depends on the fact that whether the total is 200 billion or 200 trillion, someone was bound to have rank 60 billion, just as it was guaranteed that there would be a ball numbered 7 in the urn analogy.

[7] We lack the space for a full discussion of these constraints here. For a more complete analysis, see [11].

[8] Relativizing the reference class creates a methodology that might appear to violate Bayesian conditionalization. Elsewhere, I have argued that it merely appears to do so [11].

[9] Particular applications might of course also rely on shaky empirical assumptions and might be non-compelling for that reason.

[10] Saying that the universe had to be some way or another so there is nothing to be surprised about, does not on reflection appear to be a satisfactory response [23]. We lack the space here to review the extensive philosophical and cosmological literature on the problem of fine-tuning (for the philosophical bit, see e.g. [24-30]). Instead I shall merely summarize what I see as the chief implications of the observation selection theory outlined above.

Self-Location and Observation Selection Theory

- An Advanced Introduction -

1. Introduction

2. The need for a probabilistic anthropic principle

3. Challenges for observation selection theory

4. Sketch of a solution

5. Applications

References