Self-Locating Belief in Big Worlds: Cosmology’s Missing Link to Observation*

Nick Bostrom
Oxford University
Homepage: www.nickbostrom.com

[Preprint of the paper "Self-Locating Belief in Big Worlds: Cosmology's Missing Link to Observation." Journal of Philosophy. Vol. 99, No. 12 (2002).]

 

Space is big. It is very, very big. On the currently most favored cosmological theories, we are living in an infinite world, a world that contains an infinite number of planets, stars, galaxies, and black holes. This is an implication of most “multiverse theories”, according to which our universe is just one in a vast ensemble of physically real universes. But it is also a consequence of the standard Big Bang cosmology, if combined with the assumption that our universe is open or flat, as recent evidence suggests it is. An open or flat universe – assuming the simplest topology[1] – is spatially infinite at any time and contains infinitely many planets etc.[2]

Philosophical investigations relating to the vastness of the cosmos have focused on the fine-tuning of our universe. “Fine-tuning” refers to the alleged fact that the laws of physics are such that if any of several physical constants had been even slightly different, then life would not have existed. A philosophical cottage industry has arisen from the controversies surrounding issues such as whether fine-tuning is in some sense “improbable”, whether it should be regarded as surprising[3], whether it calls out for explanation (and if so whether a multiverse theory could explain it[4], whether it suggests ways in which current physics is incomplete[5], or whether it is evidence for the hypothesis that our universe was designed[6].

Here I wish instead to address a more fundamental problem: How can vast-world cosmologies have any observational consequences at all? I will show that these cosmologies imply, or give a very high probability to, the proposition that every possible observation is in fact made. This creates a challenge: if a theory is such that for any possible human observation that we specify, the theory says that that observation will be made, then how do we test the theory? What could possibly count as negative evidence? And if all theories that share this feature are equally good at predicting the data we will get, then how can empirical evidence distinguish between them?

I call this a “challenge” because current cosmological theories clearly do have connections to observation. Cosmologists are constantly modifying and refining theories in light of empirical findings, and they are presumably not irrational in doing so. But it is a philosophical problem to account for how this is possible.

One lesson that will emerge is that we must be careful about how we construe the evidence. We know not only that such-and-such observations are made (which we shall show is impotent as a basis for evaluating Big World theories): we also know that such-and-such observations are made by us. This indexical de se component of our evidence turns out to be crucial to cosmology, and recognizing this is the first step to the solution that I shall propose.

The second step is to formulate a new methodological principle that describes the probabilistic evidential bearing of (partly) indexical information on non-indexical hypotheses.

With the expanded evidence base and the new rule, we can explain how Big World theories are testable. We will also hint at how the epistemological theory we outline is useful in other areas of philosophy and scientific methodology.

But first, let us study in more detail how things go wrong if we construe the evidence non-indexically, in the form “Such-and-such an observation is made”. We can be generous and take “an observation” in a broad sense to include the total phenomenological content present in the observer’s mind. We do not, however, at this stage take “observing” as success verb, implying the veracity of observations; but rather, we assume an internal reading of the evidence. This assumption will later be relaxed.

I. THE CONUNDRUM

Consider a random phenomenon, for instance Hawking radiation. When black holes evaporate, they do so in a random manner such that for any given physical object there is a finite (although extremely small) probability that it will be emitted by any given black hole in a given time interval. Such things as boots, computers, or ecosystems have some finite probability of popping out from a black hole. The same holds true, of course, for human bodies and human brains in particular states.[7] Assuming that mental states supervene on brain states, there is thus a finite probability that a black hole will produce a brain in a state of making any given observation. Some of the observations made by such a brains will be illusory and some will be truthful. For example, some brains produced by black holes will have the illusory of experience of reading a measurement device that does not exist. Other brains, with the same experiences, will be making veridical observations – a measurement device may materialize together with the brain and may have caused the brain to make the observation. But the point that matters here is that any observation we could make has a finite probability of being produced by any given black hole.

The probability of anything macroscopic and organized appearing from a black hole is of course minuscule. The probability of a given conscious brain-state being created is tinier still. Yet even a low-probability outcome has a high probability of occurring if the random process is repeated often enough. And that is precisely what happens in our world, if the cosmos is very vast. In the limiting case where the cosmos contains an infinite number of black holes, the probability of any given observation being made is one.[8]

There are good grounds for believing that our universe is open and contains an infinite number of black holes. Therefore, we have reason to think that any possible human observation is in fact instantiated in the actual world.[9] Evidence for the existence of a multiverse would only add further support to this proposition.

It is not necessary to invoke black holes to make this point. Any random physical phenomenon would do. It seems we don’t even have to limit the argument to quantum fluctuations. Classical thermal fluctuations could, presumably, in principle lead to the molecules in a gas cloud containing the right elements to spontaneously bump into each other so as to form a biological structure such as a human brain.

The problem is that it seems impossible to get any empirical evidence that could distinguish between various Big World theories. For any observation we make, all such theories assign a probability of one to the hypothesis that that observation is made. That means that the fact that the observation is made is no reason whatever for preferring one of these theories to the others. Experimental results appear totally irrelevant.[10]

We can see this formally as follows. Let B be the proposition that we are in a Big World, defined as one that is big enough and random enough to make it highly probable that every possible human observation is made. Let T be some theory that is compatible with B, and let E be some proposition asserting that some specific observation is made. Let P be an epistemic probability function. Bayes’s theorem states that

P(T|E&B) = P(E|T&B)P(T|B) / P(E|B).

In order to determine whether E makes a difference to the probability of T (relative to the background assumption B), we need to compute the difference P(T|E&B) - P(T|B). By some simple algebra it is easy to see that

P(T|E&B) - P(T|B)0 if and only if P(E|T&B)P(E|B).

This means that E will fail to give empirical support to T (modulo B) if E is about equally probable given T&B as it is given B. We saw above that P(E|T&B)P(E|B)1. Consequently, whether E is true or false is irrelevant for whether we should believe in T, given we know B.

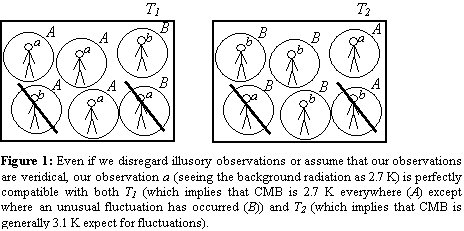
To illustrate, let T2 be some perverse permutation of an astrophysical theory T1 that we actually embrace. T2 differs from the T1 by assigning a different value to some physical constant. To be specific, let us suppose that T1 says that the temperature of the cosmic microwave background radiation is about 2.7 Kelvin (which is the observed value) whereas T2 says it is, say, 3.1 K. Suppose furthermore that both T1 and T2 imply that we are living in a Big World. One would have thought that our experimental evidence favors T1 over T2. Yet the above argument seems to show that this view is mistaken. Our observational evidence supports T2 just as much as T1. We really have no reason to think that the background radiation is 2.7 K rather than 3.1 K.

II. IT’S NOT THE OLD POINT ABOUT UNDERDETERMINATION OF THEORY BY DATA

At first blush, it could seem as if this simply rehashes the lesson, made familiar by Duhem and Quine, that it is always possible to rescue a theory from falsification by modifying some auxiliary assumption, so that strictly speaking no scientific theory ever implies any observational consequences. The above argument would then merely have provided an illustration of how this general result applies to cosmological theories. However, this would be to miss the point.

If the argument given above is correct, it establishes a much more radical conclusion. It purports to show that all Big World theories are not only logically compatible with any observational evidence, but they are also perfectly probabilistically compatible. They all give the same conditional probability (namely one) to every observation statement E defined as above. This entails that no such observation statement can have any bearing, whether logical or probabilistic, on whether the theory is true. If that were the case, it would not seem worthwhile to make astronomical observations if what we are interested in is determining which Big World theory to favor. The only reasons we could have for choosing between such theories would be either a priori (simplicity, elegance, etc.) or pragmatic (such as ease of calculation).

Nor is the argument making the ancient statement that human epistemic faculties are fallible, that we can never be certain that we are not dreaming or are brains in a vat. No, the point here is not that such illusions could occur, but rather that we have reason to believe that they do occur, not just some of them but all possible ones. In other words, we can be fairly confident that the observations we make, along with all possible observations we could make in the future, are being made by brains in vats and by humans that have spontaneously materialized from black holes or from thermal fluctuations. The argument would entail that this abundance of observations makes it impossible to derive distinguishing observational consequences from contemporary cosmological theories.

III. THE CONCLUSION IS A REDUCTIO

I trust that most readers will find this conclusion unacceptable. Cosmologists certainly appear to be doing experimental work and modify their theories in light of new empirical findings. The COBE satellite, the Hubble Space Telescope, and other devices are showering us with data that have been causing something of a renaissance in the world of astrophysics in recent years. Yet the argument described above would show that the empirical import of this information could never go beyond the humble role of providing support for the hypothesis that we are living in a Big World, for instance by showing that the universe is open. Nothing apart from this one fact could be learnt from such observations. Once we have established that the universe is open and infinite, then any further work in observational astronomy would be a waste of time and money.

Worse still, the leaky connection between theory and observation in cosmology spills over into other domains. Since nothing hinges on how we defined T in the derivation above, the argument can easily be extended to prove that observation does not have a bearing on any scientific question so long as we assume that we are living in a Big World.[11]

This consequence is absurd, so we should look for a way to mend the methodological pipeline and restore the flow of testable observational consequences from Big World theories. How can we do that?

IV. GIVING UP THE INTERNAL CONSTRUAL OF “OBSERVATION” DOESN’T SAVE US

Suppose we give up the internal construal of “observation” and instead take the term as a success verb, so that observing, say, a blue table implies that there is a blue table that is causally responsible for the observation. Suppose further that we couple this with the postulation that we are entitled (and perhaps even required) to have a prior credence function that strongly favors the hypothesis that we for the most part really do observe (in the success sense) what it seems to us that we are observing. Then it might appear as if we have an exit from our predicament. (Alternatively, we could formulate this escape plan by sticking to the original internal definition of “observation” and adding the postulate that our prior credence functions should strongly favor the veridicality of our observations.)

However, even setting aside foundationalist scruples, the proposed solution doesn’t get us out of the pickle.

To see this, consider that observers are not the only things that have a finite probability of being generated in random systems. On the same ground that we should expect human observers in all possible states to be ejected from black holes or to form from vastly improbable thermal fluctuations, we should also expect all physically possible local environments to spring forth. So not only are there observers having all sorts of illusions (of seeing a blue table or reading a measurement apparatus) but additionally there are observers making all sorts of veridical observations (actually seeing a blue table or reading off instruments in each of their possible output states). Consequently, even if we assume our observations to be veridical, we are still left with the problem that our current best theories give probability one to the existence of all possible such observations together with their truth-making local environments. (See Figure 1). We can even press on to the conclusion that for any possible human observation, there may be habitats in which that observation is appropriately caused by the observed object and in which the observer’s perceptions in general track her surroundings.[12]

A qualification is due. While small-scale environments, e.g. ones that include tables and measuring apparatuses, are on a par with human bodies, it is not clear that very large systems such as galactic superclusters could be produced by any of the random processes that we have discussed. If we stipulate that we are making veridical observations of these mega-scale entities, we could thus salvage the testability of some aspects of cosmological theories that concern these large-scale entities. Yet this would be of little avail since it would not rescue the rest of our epistemic practices, which deal with medium-sized and small things. Observations of such items would still be subject to the charge of being radically irrelevant to our theories about the world, modulo the Big World hypothesis.[13]

A further shortcoming of the proposal (apart from the fact that it doesn’t work) is that it doesn’t tell us anything about the defeasibility conditions of the purported principle that you should be strongly biased in favor of the veridicality of your observations. Clearly, there are cases where it would be unreasonable to believe that one’s observations are veridical. For example, if you knew that almost all observers in your current situation (tucked in, let’s say, between the bedsheets in a detox unit with the sensation of bugs crawling under your skin) were hallucinating, then you should not believe that your current observations are veridical, unless you had additional information defeating that conclusion. A satisfactory account of the Big World case ought to have at least something to say about why the presence of lots of hallucinating and otherwise misled observers in Big Worlds does not undermine our confidence in the reliability of our own observations while the contrary holds specifically for clients in the methadone clinic and other such special situations.

So if an externalist construal of the evidence is not the answer, what is?

V. RESTORING THE FLOW OF TESTABLE CONSEQUENCES VIA A LIMITED INDIFFERENCE PRINCIPLE OVER DE SE STATEMENTS

It may seem as if our troubles originate from the somewhat “technical” point that in a large enough cosmos, every observation will be made by some freakish observers here and there. It remains the case, however, that those observers are exceedingly rare and far between. For every observation made by a freak observer spontaneously materializing from Hawking radiation or thermal fluctuations, there are trillions upon trillions of observations made by regular observers who have evolved on planets like our own and who make veridical observations of the universe. Why can we not solve the problem, then, by saying that although all these freak observers exist and are suffering from various illusions (or are making veridical but unrepresentative observations), it is highly unlikely that we are among their numbers? Then we should think, rather, that we are very probably one of the regular observers whose observations reflect reality. We could safely ignore the freak observers and their illusions and misleading perceptions in most contexts when doing science.

In my view, this response suggests the right way to proceed. Because the freak observers are in such a tiny minority, their observations can be disregarded for most purposes. It is possible that we are freak observers – we should assign to that hypothesis some finite probability, but such a tiny one that it does not make any practical difference.

If we want to run with this idea, it is crucial that we construe our evidence differently than we did above. If our evidence is simply “Such and such an observation is made” then the evidence has probability one given any Big World theory – and we ram our heads straight into the problems I described. But if we construe our evidence in the more specific form “We are making such and such observations” then we have a way out. For we can then say that although Big World theories make it probable that some such observations be made, they need not make it probable that we should be the ones making them.

Let us therefore define:

E’ := “Such and such observations are made by us”

E’ contains an indexical de se component that the original evidence-statement we considered, E, did not. E’ is logically stronger than E. The rationality requirement that one should take all relevant evidence into account dictates that in case E’ leads to different conclusions than does E, then it is E’ that determines what we ought to believe.

A question that now arises is how to determine the evidential bearing that statements of the form of E’ have on cosmological theories. Using Bayes’s theorem, we can turn the question around and ask, how do we evaluate P(E’|T&B), the conditional probability that a Big World theory gives to us making certain observations? The argument in the foregoing sections showed that if we hope to be able to derive any empirical implications from Big World theories, then P(E’|T&B) should not generally be set to unity or close to unity. P(E’|T&B) must take on values that depend on the particular theory and the particular evidence that we are we are considering. Some theories T are supported by some evidence E’; for these choices P(E’|T&B) is relatively large. For other choices of E’ and T, the conditional probability will be much smaller.

To be concrete, consider the two rival theories T1 and T2 about the temperature of the cosmic microwave background. Let E’ be the proposition that we have made those observations that cosmologists innocently take to support T1. E’ includes readings from radio telescopes etc. Intuitively, we want P(E’|T1&B) > P(E’|T2&B). That inequality must be the reason why cosmologists believe that the background radiation is in accordance with T1 rather than T2, since a priori there is no ground for assigning T1 a substantially greater probability than T2.

A natural way to achieve this result is by postulating that we should think of ourselves as being in some sense “random” observers. Here we use the idea that the essential difference between T1 and T2 is that the fraction of observers that would be making observations in agreement with E’ is enormously greater on T1 than on T2. If we reason as if we were randomly selected samples from the set of all observers, or from some suitable subset thereof, then we can explicate the conditional probability P(E’|T&B) in terms of the expected fraction of all observers in the reference class that the conjunction of T and B says would be making the kind of observations that E’ says that we are making. As we shall see, this postulate enables us to conclude that P(E’|T1&B) > P(E’|T2&B).

Let us call this postulate the Self-Sampling Assumption:

(SSA) Observers should reason as if they were a random sample from the set of all observers in their reference class.

The general problem of how to define the reference class is complicated, and I shall not address it here. For the purposes of this paper we can think of the reference class as consisting of all observers who will ever have existed. We can also assume a uniform sampling density over this reference class. Moreover, it simplifies things if we set aside complications arising from assigning probabilities over infinite domains by assuming that B entails that the number of observers is finite, albeit such a large finite number that the problems described above obtain. These assumptions help us focus on basic principles.

Here is how SSA supplies the missing link needed to connect theories like T1 and T2 to observation. On T2, the only observers who observe an apparent temperature of the cosmic microwave background CMB2.7 K are those who either have various sorts of rare illusions (for example because their brains have been generated by black holes and are therefore not attuned to the world they are living in) or happen to be located in extremely atypical places (where e. g. a thermal fluctuation has led to a locally elevated CMB temperature). On T1, by contrast, almost every observer who makes the appropriate astronomical measurements and is not deluded will observe CMB2.7 K. A much greater fraction of the observers in the reference class observe CMB2.7 K if T1 is true than if T2 is true. By SSA, we consider ourselves as random observers; so it follows that on T1 we would be much more likely to find ourselves as one of those observers who observe CMB2.7 K than we would on T2. Therefore, P(E’|T1&B) >> P(E’| T2&B). Supposing that the prior probabilities of T1 and T2 are roughly the same, P(T1)P(T2), it is then trivial to derive via Bayes’s theorem that P(T1|E’&B) > P(T2|E’&B). This vindicates the intuitive view that we do have empirical evidence that favors T1 over T2.

The job that SSA is doing in this derivation is to enable the step from a proposition about fractions of observers to propositions about corresponding probabilities. We get the propositions about fractions of observers by analyzing T1 and T2 and combining them with relevant background information B; from this we conclude that there would be an extremely small fraction of observers observing CMB2.7 K given T2 and a much larger fraction given T1. We then consider the evidence E’, which is that we are observing CMB2.7 K. SSA authorizes us to think of the “we” as a kind of random variable ranging over the class of actual observers. From this it then follows that E’ is more probable given T1 than given T2. But without assuming SSA, all we can say is that a greater fraction of observers observe CMB2.7 K if T1 is true, and at that point the argument would grind to a halt. We could not reach the conclusion that T1 is supported over T2. For this reason I propose that SSA, or something like it, be adopted as a methodological principle.

It may seem mysterious how probabilities of this sort can exist – how can we possibly make sense of the idea that there was some chance that we might have been other observers than we are? However, what I am suggesting here is not the existence of some objective, or physical, chances. I am not suggesting that there is a physical randomization mechanism, a cosmic fortune wheel as it were, that assigns souls to bodies in a stochastic manner. Rather, we should think of these probabilities as epistemic. They are part of a proposal explicating the epistemic relations that hold between theories (such as T1 and T2) and evidence (such as E’) containing a de se component. We can view SSA as a kind of restricted indifference principle that applies to credences over de se propositions, or sets of centered possible worlds in the Quinean terminology. The status of SSA could also be regarded as in some respects akin to that of the David Lewis’s Principal Principle[14], which expresses a connection between physical chance and epistemic credence. Crudely put, the Principal Principle says that if you know that the objective (physical) chance of some outcome A is x%, then you should assign a credence of x% to A (unless you have additional “inadmissible” information). Analogously, SSA can be read as saying that if you know that a fraction x% of all observers in your reference class are in some type of position A, then you should assign a prior credence of x% to being in a type-A position. This prior credence must, of course, be conditionalized on any other relevant information you have in order to get the posterior credence, i.e. the degrees of belief you should actually have given all you know. Thus, after conditionalizing on the observation that CMB2.7 K, you get, trivially, a posterior function that assigns zero credence to the hypothesis that you are an observer that observes CMB3.1 K. But it is the higher conditional prior credence (according to SSA) of observing that CMB2.7 K given T1 than given T2 that renders it the case that conditionalizing on this observation preferentially supports T1.

VI. AN ILLUSTRATION

We can illustrate how SSA works by a simple thought experiment.

Blackbeards and Whitebeards.

In an otherwise empty world there are three rooms. God tosses a fair coin and creates three observers as a result, placing them in different rooms. If the coin falls heads, He creates two observers with black beards and one with a white beard. If it falls tails, it is the other way around: He creates two whitebeards and one blackbeard. All observers are aware of these conditions. There is a mirror in each room, so observers know the color of their own beard. You find yourself in one of the rooms and you see that you have a black beard. What credence should you give to the hypothesis that the coin fell heads?

The situation is depicted in Figure 2.

Because of the direct analogy to the cosmology case, we know that the answer must be that you should assign a greater credence to Heads than to Tails. Let us apply SSA and see how we get this result.

From the setup, we know that the prior probability of Heads is 50%. This is the probability you should assign to Heads before you have looked in the mirror and thus before you know your beard color. That this probability is 50% follows from the Principal Principle together with the fact you know that the coin toss was fair. We thus have

Next we consider the conditional probability of you observing that you have black beard given a specific outcome of the toss. If the coin fell heads, then two out of three observers observe themselves having a black beard. If the coin fell tails, then one out of three observe having a black beard. By SSA, you reason as if you were a randomly sampled observer, giving

.

Using Bayes’s theorem, we can then calculate the conditional probability of Heads given that you have a black beard:

     .

After looking in the mirror and learning that your beard is black you should therefore assign a credence of  to Heads and  to Tails.

This result mirrors that of the cosmology example. Because one theory (T1, Heads) entails that a greater fraction of all observers are observing what you are observing (E’, Black) than does another theory (T2, Tails), the former theory obtains preferential support from your observation.

VII. SUMMARY: WE NEED A METHODOLOGY FOR EVIDENCE WITH A DE SE COMPONENT

Big World theories, popular in contemporary cosmology, engender a peculiar methodological problem: because they say the world is very big and somewhat stochastic, they imply (or make it highly probable) that every possible human observation is made. The difficulty is that it is unclear how we could ever have empirical reasons for preferring one such theory to another, since they all seem to fit equally well with whatever we observe. This skeptical threat is different from and much more radical than the problem of underdetermination of theory by data associated with Duhem and Quine. And if left unfixed, the broken connection between observation and theory spills over from cosmology into other domains.

We saw that the leakage cannot be stopped even by blocking all consideration given to the possibility of illusory observations, because the maverick observations made in Big Worlds include veridical ones as well as illusions. Instead, we proposed to repair methodology by means of a new epistemic principle, the Self-Sampling Assumption, which takes into account the de se component of our evidence. This principle connects Big World theories to observation in an intuitively plausible way and vindicates the practices of cosmologists who test hypotheses against experimental findings.

The Self-Sampling Assumption has implications in other problem areas in science and philosophy. It can be seen as an explication of the anthropic principle, understood in the original spirit of by Brandon Carter, a theoretical physicist whose seminal work opened the door to a systematic exploration of observation selection effects.[15] Observation selection effects are a kind of bias that may be present in our data that is not due to limitations in our measurement apparatuses but to the fact that our data are preconditioned on the existence of a suitably positioned observer to “have” the data (and to build the instruments in the first place). Carter investigated the relevance of observation selection effects for attempts to evaluate the bearing of our current evidence on questions such as how improbable it is for complex life forms to evolve on a given Earth-like planet or how many critical improbable steps were involved in our evolution.[16] To illustrate, take one of the simplest points Carter made: Even if a theory says that the probability for an Earth-like planet of giving rise to intelligent life is small, the theory will still perfectly fit our observation of intelligent life having evolved on this planet provided that the total number of Earth-like planets is large enough for it to have been probable, according to the theory, that intelligent life should arise somewhere.

Similar modes of reasoning are invoked in some discussions of no-collapse versions of quantum mechanics[17] and, as hinted at in the introduction, they play a central role in the debate about the significance of the apparent fine-tuning of our universe and the capacity of multiverse theories to explain it. Even an application to traffic planning has been discovered.[18] On the more theoretical side, we have game theoretic problems involving imperfect recall, such as the Absent-Minded Driver problem[19] and its philosophical, more purely epistemic analogue, the Sleeping Beauty problem[20].

What these various topics have in common is that they involve the assignment of conditional credences to statements of the form “I make such and such observations given that the world is such and such.”[21] In other words, they involve the evaluation of a de se component of our evidence: our knowledge that we are the ones making a certain observation or that we are the ones who have a certain piece of (otherwise non-indexical) evidence. Our duty to objectivity must not be misunderstood as a license to ignore de se clues. The considerations advanced in this paper impose constraints on what can count as a satisfactory methodology for fashioning knowledge out of this indexical part our epistemic raw material. Such a methodology, a general theory of observation selection effects and its various scientific and philosophical applications, is something I have attempted to set forth elsewhere.[22]


Footnotes

* I’m grateful for valuable comments from Craig Callender, Milan Cirkovic, Adam Elga, Colin Howson, John Leslie, Peter Milne, Don Page, Elliott Sober, Alex Vilenkin, Roger White, and three anonymous referees.
[1] I.e. that space is simply connected. There is a recent burst of interest in the possibility that our universe might be multiply connected, in which case it could be both finite and hyperbolic. A multiply connected space could lead to a telltale pattern consisting of a superposition of multiple images of the night sky seen at varying distances from Earth (roughly, one image for each lap around the universe that the light has traveled). Such a pattern has not been found, although the search continues. For an introduction to multiply connected topologies in cosmology, see M. Lachièze-Rey and J.-P. Luminet, J.-P., “Cosmic Topology,” Physics Reports, 254(3) (1995): 135-214.
[2] A widespread misconception is that the open universe in the standard Big Bang model becomes spatially infinite only in the temporal limit. The observable universe is finite, but only a small part of the whole is observable (by us). One fallacious intuition that might be responsible for this misconception is that the universe came into existence at some spatial point in the Big Bang. A better way of picturing things is to imagine space as an infinite rubber sheet, and gravitationally bound groupings (such as stars and galaxies) as buttons glued on to it. As we move forward in time, the sheet is stretched in all directions so that the separation between the buttons increases. Going backwards in time, we imagine the buttons coming closer together until, at “time zero”, the density of the (still spatially infinite) universe becomes infinite everywhere. See e.g. J. L. Martin, General Relativity (London: Prentice Hall, 1995).
[3] E.g. J. Earman, “The SAP also Rises: A Critical Examination of the Anthropic principle,” Philosophical Quarterly, 24(4) (1987): 307-317; J. Leslie, J., Universes (London: Routledge, 1989).
[4] E.g. Q. Smith, “Anthropic Explanations in Cosmology,” Australasian Journal of Philosophy 72(3) (1994): 371-382; I. Hacking, “The Inverse Gambler’s Fallacy: The Argument from Design. The Anthropic Principle Applied to Wheeler Universes,” Mind 76 (1987): 331-340.
[5] E.g. E. McMullin, “Indifference Principle and Anthropic Principle in Cosmology,” Studies in History and Philosophy of Science, 24(3) (1993): 359-389.
[6] E.g. R. Swinburne, “Argument from the Fine-tuning of the Universe,” in Physical Cosmology and Philosophy, ed. J. Leslie and J. Collier (New York: Macmillan, 1990): pp. 154-173.
[7] See e.g. S. Hawking and W. Israel, eds., General Relativity: An Einstein Centenary Survey (Cambridge University Press, 1979): “[I]t is possible for a black hole to emit a television set or Charles Darwin” (p. 19). To avoid making a controversial claim about personal identity, Hawking and Israel ought to have weakened this to “… an exact replica of Charles Darwin”. But see also G. J. Belot et al., “The Hawking Information Loss Paradox: The Anatomy of a Controversy,” British Journal for the Philosophy of Science 50(2) (1999): 189-229.
[8] In fact, there is a probability of unity that infinitely many tokens of each observation-type will appear. But one of each suffices for present purposes.
[9] I restrict the assertion to human observations in order to avoid questions as to whether there may be other kinds of possible observations that perhaps could have infinite complexity or be of some alien or divine nature that does not supervene on stuff that is emitted from black holes – such stuff is physical and of finite size and energy.
[10] Some cosmologists are recently becoming aware of the problematic that this paper describes (e.g. A. Vilenkin, “Unambiguous probabilities in an eternally inflating universe.” Physical Review Letters, 81 (1998): 5501-5504; A. Linde and A. Mezhlumian, “On Regularization Scheme Dependence of Predictions in Inflationary Cosmology,” Physical Review D, 53 (1996): 4267-4274. See also J. Leslie, “Time and the Anthropic Principle,” Mind 101(403) (1992): 521-540.
[11] And were it really true that we have no means of testing Big World theories, then it is not even clear that the empirical support we currently have for such theories could be maintained. Such theories would seem self-undermining in that they would say of their own evidence, in effect, that it was not to be trusted.
[12] I want to emphasize that the problem is not that there is some massive inconsistency of contradictory observations. To assert the existence of all possible human observations is not inconsistent, since the observations may be illusory. Moreover, even if all the observations were asserted to be veridical, it would still be no inconsistency, since the various diverse properties that are being observed may be instantiated at different places, just as a tie can be both blue and yellow (although not at the same spot at the same time). Rather, the problem is how to derive testable predictions given our inability to observationally locate ourselves in a Big World, which is rather analogous to seeing a yellow spot through a microscope and not knowing which part of the hypothesized tie we are looking at.
[13] We may also note that there are some (speculative) theories according to which even the largest structures that we see are not large enough to escape the problem (e.g. M. Tegmark, “Does the universe in fact contain almost no information?” Foundations of Physics Letters, 9(1) (1996): 25-42). Moreover, there are many much less extreme theories, such as chaotic inflation theory (see e.g. A. Linde, “Inflation with variable Omega,” Physics Letters B, 351 (1995): 99-104), according to which observers are observing a wide range of different values of some physical constant and parameters, not because the observers have illusions or live in habitats that originate from black holes or the like, but because the “constants” and parameters vary over vast cosmic distances or epochs.
[14] See e.g. D. Lewis, Philosophical Papers II (Oxford, 1986) and “Humean Supervenience Debugged,” Mind, 103(412) (1994): 473-490. A similar principle had earlier been introduced by Hugh Mellor in The Matter of Chance (Cambridge, 1971).
[15] “Large Number Coincidences and the Anthropic Principle in Cosmology,” in Confrontation of Cosmological Theories with Data, ed. M. S. Longair (Dordrecht: Leidel, 1973): pp. 291-298; “The Anthropic Selection Principle and the Ultra-Darwinian Synthesis,” in The Anthropic Principle, eds. F. Bertola and U. Curi (Cambridge, 1989): pp. 33-63.
[16] “The Anthropic Principle and its Implications for Biological Evolution,” Philosophical Transactions of the Royal Society, A 310 (1983): 347-363.
[17] See e.g. D. N. Page, “Can Quantum Cosmology Give Observational Consequences of Many-Worlds Quantum Theory,” in General Relativity and Relativistic Astrophysics, Eighth Canadian Conference, Montreal, Quebeck, eds. C. P. Burgess and R. C. Myers (New York: American Institute of Physics, 1999), pp. 225-232.
[18] N. Bostrom, “Cars In the Next Lane Really Do Go Faster,” PLUS, 17 (2001).
[19] See e.g. M. Piccione and A. Rubinstein, “On the Interpretation of Decision Problems with Imperfect Recall,” Games and Economic Behaviour, 20 (1997): 3-24; R. J. Aumann and S. Hart et al., “The Forgetful Passenger,” Games and Economic Behaviour 20 (1997): 117-120.
[20] E. g. A. Elga, “Self-locating Belief and the Sleeping-Beauty problem,” Analysis 60(266) (2001): 143-147; D. Lewis, “Sleeping Beauty: reply to Elga,” Analysis 61(271) (2001): 171-175.
[21] Or in some cases, the analogous temporal construction: “I make such and such observations now given that the world is such and such.”
[22] Anthropic Bias: Observation Selection Effects in Science and Philosophy (New York: Routledge, 2002). A theory of observation selection effects must walk a fine line in order to cater to legitimate scientific needs while avoiding philosophical paradoxes, of which a great number lie in ambush. Incidentally, the Self-Sampling Assumption is, in my view, a mere derivative of a more powerful principle, and it is only valid in special cases.